The analysis of correlation is an extremely useful technique in business. Naturally, correlations are extremely popular in various analyses. Correlation is measured by a coefficient that is a statistical estimation of the strength of relationship between data. The most commonly used measure of correlation was given by the British mathematician, Karl Pearson, and is called the Karl Pearson’s Product Moment Coefficient of Correlation (or simply, Coefficient of Correlation), after him.
Before we look at an example to understand correlations, I want to quickly mention that there are some important assumptions made while calculating the Karl Pearson’s Coefficient of Correlation. These assumptions are discussed in more detail here.
The Story of Rice and Rainfall
I’ve gathered data about the production of rice in India between 1987 and 2003. As you may imagine, rice production would be highly dependent on the amount of monsoon rain that the country receives. The data in the table shows rice production in million tons, and the rainfall received with respect to the long period average (LPA). The LPA is the average rainfall received for 50 years starting 1951. The LPA is around 89 cm of rain.
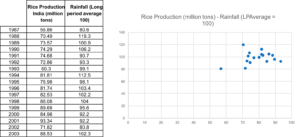
Uh, oh.. Weren’t we expecting to see a stronger correlation? The computed coefficient of correlation is 0.24565, indicating the weakly positive relationship.
What gives?
The Story of Rice without Rainfall?
Thinking a little further, we realise that modern agriculture is no longer so dependent on the vagaries of monsoon as it was in the past. Today, we have plenty of irrigation methods available to farmers that have reduced the dependence on the monsoons. Could the quantity of rice produced be related to the irrigation then? Let’s take a look:
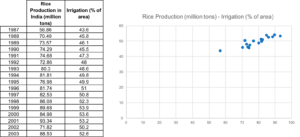
This gives us a much stronger relationship, and that is expected. The coefficient of correlation is 0.89338, indicating a strong positive correlation. Therefore, we can say that the Indian farmers are no longer completely dependent on rainfall, thanks to modern methods of irrigation!
To examine the above data using another correlation computation – Spearman’s Rank Correlation Coefficient which gives us the correlation between average ranks, instead of between the values, read this post.
Play a little game of guessing the coefficient of correlation by looking at a scatter plot. Have fun!


